Question

You fly your 15 m spaceship, parallel to the ship's length with a speed of c/3 relative to your friend. How long is your spaceship as observed by your friend?

Answer 1

We are asked to determine the length of a ship whose length is 15 meters. To determine the relative length we will use the following formula:

`L=L_0\sqrt{1-(v^2)/(c^2)}`

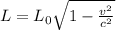
Where:

`\begin{gathered} L=\text{ relative length} \\ L_0=\text{ original length} \\ v=\text{ velocity of the object} \\ C=\text{ speed of light} \end{gathered}`

Now, we substitute the value of the speed as a function of the speed of light:

`v=(c)/(3)`

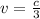
Substituting we get:

`L=L_0\sqrt{1-(((c)/(3))^2)/(c^2)}`

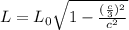
Now, we distribute the exponent and simplify:

`L=15m\sqrt{1-(1)/(9)}`

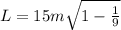
Solving the operations:

`L=14.14m`

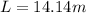
Therefore, the length of the spaceship observed by the friend is 14.14 meters.