We have the cost function C(d) and the revenue function R(d) as:
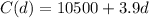
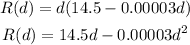
The profit can be defined as the difference between the revenue and the cost, so we can express it as:
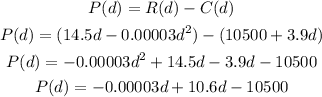
We can now evaluate it for d = 30,000 as:
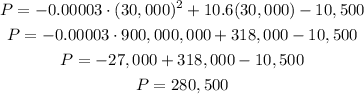
Answer: the profit for 30,000 units is $280,500 [Fourth option].