Question

Write the rule the nth term; then find a7 1) 729, -243, 81,...2) 6, -12, 24,...3) 8, 12, 18,...

Answer 1

1. 1

3. 729/8

Step-by-step explanation:

Part 1

In the sequence: 729, -243, 81,...

`\begin{gathered} (81)/(-243)=-(1)/(3) \\ -(243)/(729)=-(1)/(3) \end{gathered}`

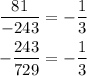
• The first term, a = 729

,

• The common ratio, r = -1/3

The nth term of a geometric progression is obtained by the formula below:

`a_n=a_1r^(n-1)`

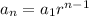
Therefore, the rule for the nth term will be:

`a_n=729(-(1)/(3))^(n-1)`

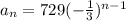
We then find a7, the seventh term.

`\begin{gathered} a_7=729(-(1)/(3))^(7-1) \\ =729(-(1)/(3))^6 \\ =729*(1)/(729) \\ =1 \end{gathered}`

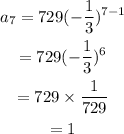
The seventh term is 1.

Part 3

In the sequence: 8, 12, 18,...​

`\begin{gathered} (12)/(8)=1.5 \\ (18)/(12)=1.5 \end{gathered}`

• The first term, a = 8

,

• The common ratio, r = 1.5

The nth term of a geometric progression is obtained by the formula below:

`a_n=a_1r^(n-1)`

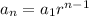
Therefore, the rule for the nth term will be:

`a_n=8(1.5)^(n-1)`

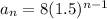
We then find a7, the seventh term.

`\begin{gathered} a_7=8(1.5)^(7-1) \\ =8(1.5)^6 \\ =(729)/(8) \\ =91(1)/(8) \end{gathered}`

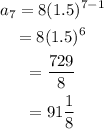
The seventh term is 729/8.