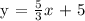Question

A linear function crosses the x-axis when x = -3 and the y-axis when y = 5. What is the equation of the line

Answer 1

The general equation of a line is expressed as

`\begin{gathered} y\text{ = mx+c ----- equation 1} \\ \text{where} \\ m\Rightarrow slope\text{ of the line} \\ c\Rightarrow y-intercept\text{ of the line} \end{gathered}`

When the linear function crosses the x-axis at x = -3, the value of y equals zero.

Thus, substitute the above parameters in equation 1.

`\begin{gathered} 0\text{ = m(-3) + c} \\ \Rightarrow-3m\text{ + c = 0 ----- equation 2} \end{gathered}`

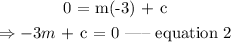
When the linear function crosses the y-axis at y = 5, the value of x equals zero.

Thus, substitute the above parameters in equation 1.

`\begin{gathered} 5\text{ = m(0) + c} \\ \Rightarrow c\text{ = 5 ------ equation 3} \end{gathered}`

From equation 3, substitute the value of 5 for c in equation 2.

Thus,

`\begin{gathered} -3m\text{ + c =0} \\ \Rightarrow-3m\text{ + 5 }=\text{ 0} \end{gathered}`

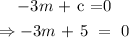
solve for m,

`\begin{gathered} -3m\text{ + 5 }=\text{ 0} \\ collect\text{ like terms} \\ -3m\text{ = 0-5} \\ -3m\text{ = -5} \\ \text{divide both sides of the equation by the coefficient of m, which is -3} \\ (-3m)/(-3)\text{ = }\frac{\text{-5}}{-3} \\ \Rightarrow m\text{ = }(5)/(3) \end{gathered}`

Since the values of m and c are now known, substitute their respective values into

equation 1.

From equation 1, we have

`\begin{gathered} y\text{ = mx + c} \\ \Rightarrow\text{ y = }(5)/(3)x\text{ + 5} \end{gathered}`

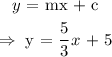
Hence, the equation of the line is

`\text{ y = }(5)/(3)x\text{ + 5}`