Question

In the xy plane, the line determined by the points (2, k) and (k, 32) passes through the origin. Which of the following could be the value of k?A) 0 B) 4C) 8D) 16

Answer 1

We know that the line goes through the points (2,k), (k,32) and the origin (0,0)

To obtain the equation of a line we only need 2 points, we can use (2,k) and (0,0) to do that:

`\begin{gathered} y-0=((k-0))/((2-0))(x-0) \\ \Rightarrow y=(k)/(2)x \end{gathered}`

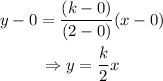
Then, we can use the third point to obtain the value of k.

`\begin{gathered} (k,32)\rightarrow y=32\Rightarrow x=k \\ \Rightarrow32=(k)/(2)\cdot k \\ \Rightarrow32\cdot2=k^2 \\ \Rightarrow k^2=64 \\ \Rightarrow k=8 \end{gathered}`

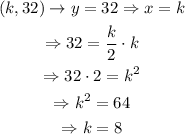
Therefore, the answer to the question is k=8, option c