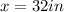1)
Given:
Required:
We need to find the value of x.
Step-by-step explanation:
Recall that the corresponding sides of similar triangles are proportional.
12m and 6m are corresponding sides of the given similar triangles
16m and x are corresponding sides of the given similar triangles
The proportion of the sides can be written as follows.
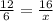
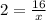
Use the cross-product method.
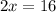
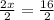
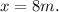
2)
Given:
18cm and 30cm are corresponding sides of the given similar triangles.
x and 25 cm are corresponding sides of the given similar triangles.
Required:
We need to find the value of x.
Step-by-step explanation:
Recall that the corresponding sides of similar triangles are proportional.
The proportion of the sides can be written as follows.
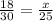
Multiply both sides of the equation by 25.
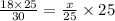
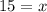
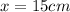
3)
Given:
x and 21m are the corresponding sides of the given similar triangles.
32m and 24m are the corresponding sides of the given similar triangles.
Required:
We need to find the value of x.
Step-by-step explanation:
Recall that the corresponding sides of similar triangles are proportional.
The proportion of the sides can be written as follows.
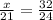
Multiply both sides of the equation by 21.
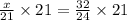
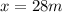
4)
Given:
12in and 15in are the corresponding sides of the given similar triangles.
x and 40in are the corresponding sides of the given similar triangles.
Required:
We need to find the value of x.
Step-by-step explanation:
Recall that the corresponding sides of similar triangles are proportional.
The proportion of the sides can be written as follows.
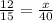
Multiply both sides of the equation by 40.
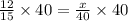
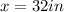
Final answer:
1)
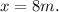
2)
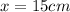
3)
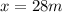
4)