First, we can make a drawing to better understand the information given:
We need to find the height of Mount Rushmore, represented by x in the drawing.
We can identify that we have a right triangle, therefore we can use the trigonometry relationships of the right triangle.
We have from the small triangle,
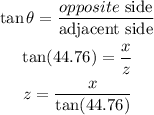
And from the big triangle we have,
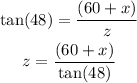
Now we can equate both equations and solve for x:

Answer: The height of Mount Rushmore is about 500 ft.