We will need to find each angles
Using cosine formula
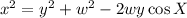
From the question given,
x=11 y=5 w=7
Substitute the values into the formula and solve for angle X
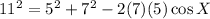
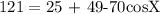
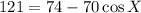
subtract 74 from both-side
121-74 = -70cosX
47 =- 70 cos X
Divide both-side by -70
(-0.6714) = cos X
Take the cos⁻' of both-side
cos⁻' (-0.6714) = X
X= 132.175
Next
Using the cosine formula
y² = x² + w² - 2xw cosY
5² =11² + 7² - 2(11)(7) - cos Y
25 = 121 + 49 - 154 cos Y
25 = 170 -