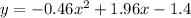Question

How to find the equation of a parabola using 3 given pointsy- intercept : (0, -1.4)x-intercept : (0.905,0)3rd point: (3.07,0.314)

Answer 1

The standard form of a quadratic equation is given below as

`y=ax^2+bx+c`

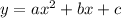
The y-intercept given is

`(0,-1.4)`

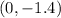
This indicates that at x=0, y= 1.4

Substitute x=0, y= 1.4 in the quadratic expression below

`\begin{gathered} y=ax^2+bx+c \\ a(0)^2+b(0)+c=-1.4 \\ c=1.4 \end{gathered}`

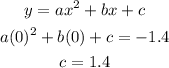
The x-intercept is given below as

`(0.905,0)`

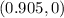
This means at x=0.905,y=0

Substitute x=0.905,y=0 in the quadratic expression above

`\begin{gathered} y=ax^2+bx+c \\ 0=a(0.905)^2+b(0.905)+c \\ \text{recall that:} \\ c=-1.4 \\ 0=a(0.905)^2+b(0.905)+c \\ 0=a(0.905)^2+b(0.905)-1.4 \\ 0.819a+0.905b=1.4----(1) \end{gathered}`

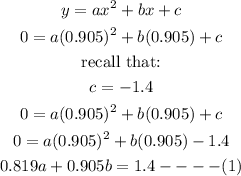
Since the third points below pass through the parabola, the third point is given below as

`(3.07,0.314)`

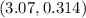
Substitute when x=3.07,y=0.314 in the quadratic expression above

`\begin{gathered} y=ax^2+bx+c \\ a(3.07)^2+b(3.07)-1.4=0.314 \\ 9.425a+3.07b=0.314+1.4 \\ 9.425a+3.07b=1.714-----(2) \end{gathered}`

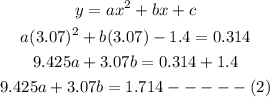
Combine equations (1) and (2) and solve simultaneously

`\begin{gathered} 0.819a+0.905b=1.4 \\ 9.425a+3.07b=1.714 \\ \text{mulipy equation (1) by 9.425 and equation 2 by 0.819} \\ 7.719a+8.53b=13.195 \\ 7.719a+2.514b=1.404 \\ \text{substracting both equations, we will have} \end{gathered}`
`\begin{gathered} 7.719a-7.719a+8.53b-2.514b=13.195-1.404 \\ (6.016b)/(6.016)=(11.791)/(6.016) \\ b=1.96 \end{gathered}`

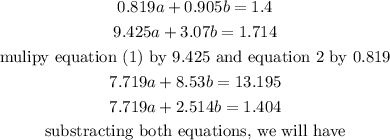
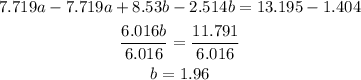
Substitute the value of b=1.96 in the equation (1)

`\begin{gathered} 0.819a+0.905b=1.4 \\ 0.819a+0.905(1.96)=1.4 \\ 0.819a+1.7738=1.4 \\ 0.819a=1.4-1.7738 \\ (0.819a)/(0.819)=(-0.3738)/(0.819) \\ a=-0.46 \end{gathered}`

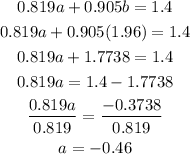
Hence,

The general equation will be

`y=-0.46x^2+1.96x-1.4`