Question

Keith stepped onto an escalator moving at a constant rate. The table below shows his distance from the first floor after different amounts of time.

Answer 1

Given the table:

Time (seconds) 6 9 12 15

Distance (cm) 980 890 800 710

Using the given table which shows Keith distance in an escalator, let's answer the following questions:

• (a). Kieth's distance from the first floor.

Let's first create an equation which represents this situation.

Apply the slope-intercept form:

y = mx + b

Where m is the rate of change while b is the initial value(distance).

To find the rate of change, apply the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

Take two points from the table:

(x1, y1) ==> (6, 980)

(x2, y2) ==> (9, 890)

Plug the values into the formula and solve for m:

`\begin{gathered} m=(890-980)/(9-6) \\ \\ m=(-90)/(3) \\ \\ m=-30 \end{gathered}`

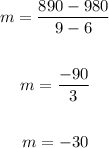
The rate of change is, m = -30.

Now, we have:

`y=-30x+b`

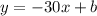
Plug in the coordinates of one point for the values of x and y respectively and solve for b.

Take the second point:

(9, 890)

`\begin{gathered} 890=-30(9)+b \\ \\ 890=-270+b \\ \\ b=890+270 \\ \\ b=1160 \end{gathered}`

Therefore, the Keith's distance from the first floor when he stepped onto the escalator is:

1160 centimetes.

(b). From the table, we can see that as the time increases, the distance decrease.

This means that as the time increases, his distance from the first floor decreases.

The rate at which his distance from the first floor is decreasing is 30 centimeters per second.

ANSWER:

(a). 1160 centimeters

(b). As time increases, his distance from the f