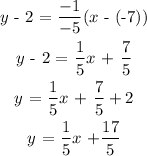Answer:
The equation parallel to the line is y = -5x - 33
The equation perpendicular to the line is:

Explanations:
The equation parallel to the line y = mx + c and passing through the point
(x₁, y₁) is given as:
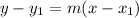
The equation perpendicular to the line y = mx + c and passing through the point
(x₁, y₁) is given as:

Comapring the line y = -5x + 8 to y = mx + c:
m = -5
The line parallel to the line y = -5x+8 and passing through the point (-7, 2) will be:

The line perpendicular to the line above and passing through the point (-7, 2) will be: