Answer: the new pressure of the gas is 15.55 atm, which is approximately 16 atm.
Step-by-step explanation:
The question requires us to determine the new pressure of the gas, given the new temperature and volume of the gas.
The following information was provided by the question:
initial temperature = T1 = 35 K
inital volume = V1 = 26 L
initial pressure = P1 = 25 atm
final temperature = T2 = 67 K
final volume = V2 = 80 L
Since both temperature and volume changed from the initial and final condition, we'll need to use the inital values given (T1, V1 and P1) to determine the number of moles of the gas (as this value does not change), and then use this value, together with the final values given (T2 and V2), to determine the new pressure.
We'll apply the equation for ideal gases to solve this problem:
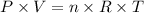
1) Calculating the number of moles of gas
We can rearrange the equation of ideal gases to calculate the number of moles:
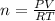
We can use the constant of gases, R, as 0.082057 L.atm/K.mol.
Applying the values given by the question, we'll have:
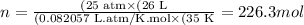
Therefore, there are 226.3 moles of the gas.
2) Calculating the new pressure
Next, with the amount of moles of gas known, we can calculate the new pressure of the gas.
We can rearrange the equation of ideal gases to calculate the pressure:
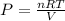
And, applying the values provided by the question:
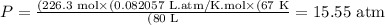
Therefore, the new pressure of the gas is 15.55 atm.