If a polynomial can be factored as the product of k linear factors with exponents n₁, n₂, ..., n_k, as follows:
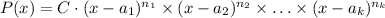
Then, the zeros of P(x) are a₁, a₂, ...,a_k and their respective multiplicities are n₁, n₂, ..., n_k.
For the given polynomial, notice that 3x^2 is a common factor for all three terms. Then, factor it out:
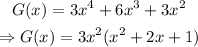
The factor (x^2+2x+1) is a perfect square binomial that can be expressed as a binomial squared:
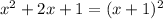
Then, G(x) can be written as:
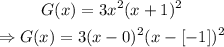
As we can see from the expression, the roots of G(x) from the smallest to largest are -1 and 0, and the multiplicities are 2 in both cases.
Therefore, the first zero is -1 with a multiplicity of 2, and the second zero is 0 with a multiplicity of 2.