We are given that a plane covers a distance of 346 miles in 2 1/4 hours. And we are asked to determine the ratio between distance and time. To do that we will divide the total distance over the amount of time, like this:
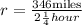
Now, the time is expressed as a mixed fraction. We can rewrite it as a fraction using the following relationship:
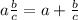
Applying the relationship we get:
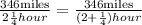
Now, we add the fractions:
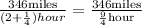
Simplifying we get:
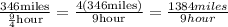
Now, solving the operation we get the unit rate:
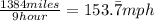
Therefore, the unit rate is 157.7 mph.