The unit circle is a circle centered at origin with radius 1. The values of the circle depends on the values of the angle created.
Below, we show the unit circle:
The x coordinate and y coordinate will make up a right triangle that has a hypotenuse of 1.
We can use the Pythagorean Theorem to write it as:
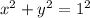
The x is what we want and y is already given. Let's substitute and find the value of x:
![\begin{gathered} x^2+y^2=1 \\ x^2+(\frac{\sqrt[]{3}}{3})^2=1 \\ x^2+(3)/(9)=1 \\ x^2+(1)/(3)=1 \\ x^2=1-(1)/(3) \\ x^2=(2)/(3) \\ x=\sqrt[]{(2)/(3)} \\ x=\frac{\sqrt[]{2}}{\sqrt[]{3}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aemnvjomazdpnqevc2ijputbrg5e03slhv.png)
This isn't one of the answer choices, so we simplify it further to match one of the answer choices. let's multiply it with Sqrt(3) OVER Sqrt(3).
Thus,
![\begin{gathered} x=\frac{\sqrt[]{2}}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}} \\ x=\frac{\sqrt[]{6}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l34xz55u49a9o2o67jsb6zhhco7llpcewz.png)
Correct Answer is B