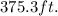Determine the horizontal distance between the technician and the base of the telephone pole to the nearest tenth of a foot .

Question

asked Apr 15, 2023 76.8k views

1 Answer

Arkmetal · Answer 1 · 2023-04-21T17:24:14+0000

To solve this problem, we will use the trigonometric function tangent, recall that, by definition in a right triangle:

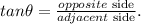
$tan\theta=\frac{opposite\text{ side}}{adjacent\text{ side}}.$

In the given triangle:

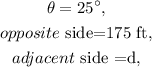
$\begin{gathered} \theta=25^(\circ), \\ opposite\text{ side=175 ft,} \\ adjacent\text{ side =d,} \end{gathered}$

where d is the distance we are looking for. Therefore:

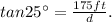
$tan25^(\circ)=(175ft)/(d).$

Solving the above equation for d, we get:

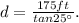
$d=(175ft)/(tan25^(\circ)).$

Finally, we get:

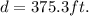
Answer:

$\begin{equation*} 375.3ft. \end{equation*}$