We have to calculate how much it would take Carolyn to to the job.
We have to use the concept of "capacity".
This would represent the amount of work each can done per unit of time.
For example, Tyler can do a job in 10 hours, so we can express the capacity of Tyler as:
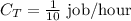
When both Carolyn and Tyler do the job, they do it in 7 hours, so we can add the capacities of both:
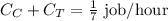
Then, as we know the capacity of Tyler, we can calculate the capacity of Carolyn as:
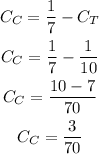
We can now use the capacity of Carolyn to calculate how much time it would take her to do the job alone:
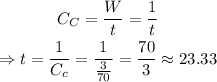
Answer: It would take Carolyn approximately 23.33 hours to do the job alone.