Step-by-step explanation:
Unit conversions make use of the idea of the multiplicative identity element: multiplying by 1 does not change the value. In general, you multiply by a fraction whose numerator is the unit you want, and whose denominator is the unit you want to cancel. The fraction has a value of 1 in that its numerator is equal to its denominator. However, the units are different.
Effectively, you treat units the way you would any variable. You can multiply and divide them, raise them to a power, and cancel them. Quantities can only be added and subtracted if they have like units. (Only "like terms" can be combined. You can't add feet and inches, but you can convert feet to inches or vice versa, and then add.)
Example:
Convert 3 inches to centimeters.
We know 1 inch = 2.54 centimeters. We want units of centimeters and we want to cancel units of inches, so we will multiply by the conversion factor (fraction) ...
(2.54 cm)/(1 inch) . . . . . . . . cm in the numerator, inch in the denominator; the numerator and the denominator are exactly equal to each other
Then ...
3 in = (3 in) × (2.54 cm)/(1 in) = (3×2.54 cm·in/in) = 7.62 cm
The units in/in cancel each other, leaving units of cm.
_____
This idea works for any unit conversion. You have to recognize the sort of unit you are converting, and only use conversion factors in the same category. That is, you can convert time to time, distance to distance, energy to energy, force to force, mass to mass, volume to volume, and so on.
When it comes to distance dimensions, you can recognize that volume is the product of three linear distance dimensions, or the product of an area dimension and a linear distance dimension. Similarly, area is the product of two linear distance dimensions, or the ratio of volume to linear distance.
in³ = in×in×in = (in²)×in
There are a couple of area dimensions that you need to pay attention to.
1 acre = 43,560 ft²
1 hectare = 10,000 m²
1 barn = 10^-28 m² . . . . not entirely whimsical
There is a volume dimension that is used in real-world water measurement known as the "acre-foot". It is the quantity of water that would cover a 1-acre area to a depth of 1 foot. As you can tell from the above, ...
1 acre-foot = 1 acre × 1 foot = 43,560 ft³
__
When you get into physics and chemistry, combinations of units are given other names. For example, the unit of force is the newton (N). It is defined as ...
1 N = 1 kg·m/s²
And the unit of energy is the newton-meter or Joule,
(1 N)·(1 m) = 1 N·m = 1 J
In terms of fundamental units, 1 J = 1 kg·m²/s².
__
Sometimes you want to do a couple of unit conversions at the same time. For example, you may want to convert miles per hour to meters per second. This will involve both distance and time conversions. Here, the time units are in the denominator, so the conversion factors need to be chosen accordingly.
Example:
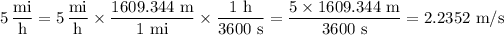
Notice that we have effectively cancelled units of miles and hours and introduced units of meters and seconds. These conversion factors are all exact, in that the numerators and denominators are exactly equal in each case.
__
When converting volume units, I often find it convenient to use linear dimension unit conversion factors to an appropriate power.
Example:
1 yd³ = ((1 yd)×(0.9144 m/yd))³ = 0.764554857984 m³
__
I like to keep the units with the numbers in this process, as I have done here. That helps me check to make sure I'm using the appropriate conversion factor appropriately. (In creating the above example, it took me a couple of iterations to realize I was erroneously computing the number of yd³ in 1 m³. Having the units right in front of me helped get it sorted.)
The usual rules for working with fractions apply. You can divide by a (rational) conversion factor in the same way you divide by any fraction: multiply by its inverse.
_____
It helps to be familiar with both US and metric units. If you're in the UK, you would want to pay attention to the definitions and conversion factors for Imperial units. SI prefixes are also helpful to memorize, as are a few other interesting relations:
1 cm³ = 1 milliliter (mL or ml) . . . . I use a capital L to avoid confusion
1000 cm³ = 1 L = 1 dm³ . . . . . . occasionally using measures in decimeters is helpful if you need final volumes in liters. Of course, ...
1 decimeter = 0.1 m = 10 cm.