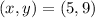Question

Solve the following system: 3x + 3y = 42 x – 3y = –22 a) No Solution b) Infinite Solutions c) (-5,-9) d) (5,9)

Answer 1

We are given the following system of equations:

`\begin{gathered} 3x+3y=42,\text{ (1)} \\ x-3y=-22\text{, (2)} \end{gathered}`

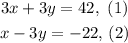
Equation (1) can be rewritten by dividing by 3 on both sides as:

`x+y=14,\text{ (1)}`

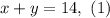
Solving for "x" in equation (1), we get:

`x=14-y`

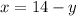
Replacing in equation (2)

`\begin{gathered} x-3y=-22 \\ 14-y-3y=-22 \end{gathered}`

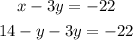
simplifying

`14-4y=-22`

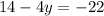
Now we solve for "y", by subtracting 14 on both sides:

`\begin{gathered} 14-14-4y=-22-14 \\ -4y=-36 \end{gathered}`

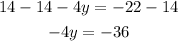
Dividing by -4 on both sides:

`y=-(36)/(-4)=9`

Replacing the value of "y" in equation (1)

`\begin{gathered} x+y=14 \\ x+9=14 \end{gathered}`

Now we subtract 9 on both sides:

`\begin{gathered} x+9-9=14-9 \\ x=5 \end{gathered}`

Therefore, the solution of the system is:

`(x,y)=(5,9)`