Question

A chef is going to use a mixture of two brands of Italian dressing. The first brand contains 9% vinegar, and the second brand contains 14% vinegar. The chef wants to make 320 milliliters of a dressing that is 13% vinegar. How much of each brand should she use?

Answer 1

Given:

First brand = 9% vinegar

Second brand = 14% vinegar

Total = 320 milliliters

Find-:

How much of each brand should she use?

Explanation-:

The total amount is 320 milliliter

Let 9% vinegar amount = x

14% vinegar amount = y

Total is 320 milliliter

then,

`\begin{gathered} x+y=320 \\ \\ y=320-x......................(1) \end{gathered}`

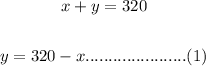
9% first and 14% second and make 13% of total

`\begin{gathered} 9\%x+14\%y=13\%\text{ of }320 \\ \\ (9)/(100)x+(14)/(100)y=(13)/(100)*320 \\ \\ 0.09x+0.14y=0.13*320 \\ \\ 0.09x+0.14y=41.6........................(2) \end{gathered}`

Put the value of "y" in eq(2) form eq(1) then,

`\begin{gathered} 0.09x+0.14y=41.6 \\ \\ 0.09x+0.17(320-x)=41.6 \\ \\ 0.09x+(0.17*320)-0.17x=41.6 \\ \\ 0.09x-0.17x+54.4=41.6 \\ \\ 0.09x-0.17x=41.6-54.4 \\ \\ -0.08x=-12.8 \\ \\ x=(-12.8)/(-0.08) \\ \\ x=160 \end{gathered}`

The value of "x" is 160.

The value of "y" is:

`\begin{gathered} x+y=320 \\ \\ y=320-x \\ \\ y=320-160 \\ \\ y=160 \end{gathered}`

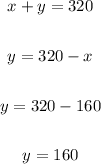
The value of "y" is 160.