We will have the following:
First, we determine the distance traveled:
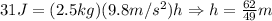
Now, we determine the time it tool to travel that distance:
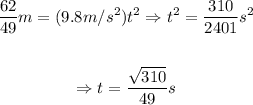
Now, we determine the velocity:
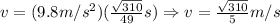
Now, we determine the kinetic energy:
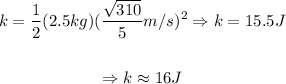
So, the kinetic energy will be approximately 16 Joules.