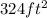Solution
The image below will be of help
The area (A) of the figure above is given by
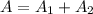
The Area A1 is a rectangle and thus, given as
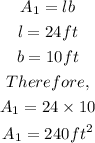
The Area (A2) is a triangle and thus, given as
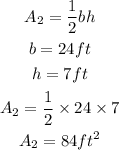
Therefore, the area will be
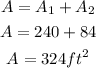
Therefore, the Area of the shaded region is