Question

Vector v has the given magnitude and direction. Find the horizontal or vertical component of v, as indicated, if θ is the direction angle of v from the horizontal. Round to the nearest tenth when necessary.

Answer 1

Step 1. We are given the magnitude and the angle of a vector v:

`\begin{gathered} Angle: \\ \alpha=66.6 \\ Magnitude: \\ |v|=31.1 \end{gathered}`

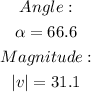
And we need to find the horizontal component of v.

The situation is represented in the following diagram:

The horizontal component will be Vx.

Step 2. To find the two components of a vector, we use the following formulas:

`\begin{gathered} v_x=|v|cos\alpha \\ v_y=|v|sin\alpha \end{gathered}`

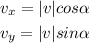
In this case, we will use the first one since we need the horizontal component.

Step 3. Substituting the known values into the formula:

`\begin{gathered} v_(x)=\lvert v\rvert cos\alpha \\ \downarrow \\ v_x=(31.1)cos(66.6) \end{gathered}`

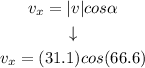
Solving the operations:

`\begin{gathered} v_x=(31.1)(0.39715) \\ v_x=12.351 \end{gathered}`

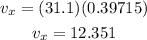
Rounding to the nearest tenth:

`v_x=12.4`

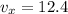
The horizontal component is 12.4

Answer: 12.4