Question

How to factor ax2+bx+c

Answer 1

To factor the expression ax² + bx + c, we can use the quadratic formula:

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where x1, and x2 are the zeros, or roots, of the polynomial. And the factored expression will be:

`ax^2+bx+c=a(x-x_1)(x-x_2)`

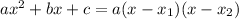
For example, if the expression is 5x² -35x + 60, then a = 5, b = -35 and c = 60. Substituting into the formula we get:

`\begin{gathered} x_(1,2)=\frac{-(-35)\pm\sqrt[]{(-35)^2-4\cdot5\cdot60}}{2\cdot5} \\ x_(1,2)=\frac{35\pm\sqrt[]{25}}{10} \\ x_1=(35+5)/(10)=4 \\ x_2=(35-5)/(10)=3 \end{gathered}`

Then, the factored expression is:

5x² -35x + 60 = 5(x - 4)(x - 3)