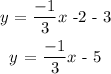Answer:
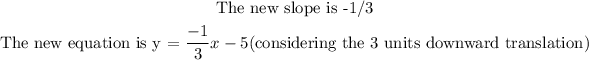
Explanations:
The general equation of a line is given by:
y = mx + c..............(1)
Where m = the slope and
c = the intercept
The first given equation is:
y = 3x - 2
Comparing the above with the general equation (i.e. equation 1)
m = 3 , c = -2
For a line to be perpendicular to another line, it must have a slope that is a negative inverse of the line:
Therefore the line that is perpendicular to line y = 3x - 2 will have a slope:
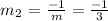
The new line that is perpendicular to the first line will have the equation:

Since the line is translated 3 units down, the equation becomes: