Question

ABOVE & BEYOND John's school is selling tickets to a spring musical. On the first day of ticket sales, the school sold 8 adult tickets and 5 child tickets for a total of $104. The school took in $80 on the second day by selling 4 adult tickets and 6 child tickets. On the third day, they sold 10 adult tickets and 4 child tickets. On the last day, they sold 22 adult tickets and 8 child tickets. How much more money did they make on the last day compared to the third day? UNIT

Answer 1

"The school sold 8 adult tickets and 5 child tickets for a total of $104", we can express it as follows

`8x+5y=104`

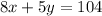
"On the second day they sold 4 adult tickets and 6 child tickets for a total of $80", we can express it as follows

`4x+6y=80`

These two equations form a linear system of equations, which we can solve by multiply the second equation by -2

`\begin{cases}8x+5y=104 \\ -8x-12y=-160\end{cases}`

Then, we combine the equations

`\begin{gathered} 8x-8x+5y-12y=104-160 \\ -7y=-56 \\ y=(-56)/(-7) \\ y=8 \end{gathered}`

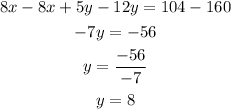
Now, we find x

`\begin{gathered} 8x+5y=104 \\ 8x+5\cdot8=104 \\ 8x=104-40 \\ x=(64)/(8) \\ x=8 \end{gathered}`

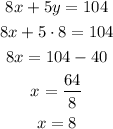
According to this solution, each adult ticket costs $8 and each child ticket costs $8.

If they sold 10 adult tickets and 4 child tickets on the third day, then they made

`10\cdot8+4\cdot8=80+32=112`

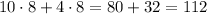
If they sold 22 adult tickets and 8 child tickets on the last day, then they made

`22\cdot8+8\cdot8=176+64=240`

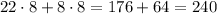
Hence, they made $128 more on the last day than the third day because that's the difference.