In order to find the probability, first let's calculate the z value with the formula below:

Using x = 98, mean = 130.7 and standard deviation = 28, we have:-
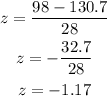
Looking at the z-table for the corresponding probability for z = -1.17, we have 0.1210, so the probability is equal to 12.1%.
This probability corresponds to the following area in the normal distribution:
The value of 0.379 in the z-table would correspond to the following area:
That is, in practical terms, it means the probability for a selected car taking between 98 seconds and 130.7 seconds (instead of the probability for lesser than 98 seconds)