The mass of the astronaut is the same no matter which planet is in.
On the other hand, the weight of the astronaut does depend on which planet is in, since each planet produces a different acceleration on the astronaut.
The formula to find the weight W of an object of mass m on a planet with acceleration g is:
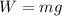
For the planet Jupiter, we have that:

For the planet Venus, we have that:
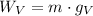
Substitute W_J=3,243.7 N and g_J=25.95 m/s^2 on the equation for Jupiter to find the mass of the astronaut:
![\begin{gathered} 3,243.7N=m\cdot(25.95(m)/(s^2)) \\ \Rightarrow m=(3,243.7N)/(25.95(m)/(s^2)) \\ =125\operatorname{kg} \end{gathered}]()
Next, substitute m=125kg and g_V=8.37 m/s^2 on the equation for Venus to find the astronaut's weight on Venus:
![\begin{gathered} W_V=(125\operatorname{kg})(8.37(m)/(s^2)) \\ =1046N \end{gathered}]()
Therefore, the astronaut's weight on Venus is 1046 N