Question

ABCD is similar to EFGH. Find the scale factor. Identify the pairs of congruent angles. Write the ratios of the corresponding side lengths in a statement of proportionality.

Answer 1

Two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal. This common ratio is called the scale factor.

The question gives that the provided shapes are similar and the statement is that:

`ABCD\sim EFGH`

This means that the corresponding angles are A and E, B and F, C and G, and D and H.

Since corresponding angles are congruent, the pair of congruent angles are:

`\begin{gathered} \angle A\cong\angle E \\ \angle B\cong\angle F \\ \angle C\cong\angle G \\ \angle D\cong\angle H \end{gathered}`

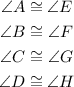
The corresponding sides will have the same ratio. The corresponding sides are AB and EF, BC and FG, CD and GH, and AD and EH.

This means that the scale factor (k) can be calculated using any one of the ratios below:

`k=(EF)/(AB)=(FG)/(BC)=(GH)/(CD)=(EH)/(AD)`

From the image, we have that:

`\begin{gathered} BC=8 \\ CD=12 \\ EH=6 \\ GH=9 \end{gathered}`

Therefore, the scale factor can be calculated using the CD and GH ratio:

`k=(GH)/(CD)=(9)/(12)=(3)/(4)`

The scale factor is 3/4.