Question

=Solve this system of equations byusing the elimination method.-X + 6y = 112x – 3y = 5([?],=

Answer 1

We have the following system of equations,

`\begin{gathered} -x+6y=11 \\ 2x-3y=5 \end{gathered}`

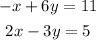
Using the elimination method.

Step #1. Multiply the 2nd equation by 2

`\begin{gathered} -x+6y=11 \\ 4x-6y=10 \end{gathered}`

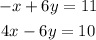
Step #2. Eliminate +6y and -6y

`\begin{gathered} -x=11 \\ 4x=10 \end{gathered}`

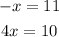
Step#3. Add the values together

`3x=21`

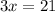
Step#4. divide both sides by 3

`x=(21)/(3)=7`

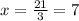
So, we have x = 7

If x=7, then,

`\begin{gathered} -7+6y=11 \\ 6y=11+7 \\ y=(18)/(6) \\ y=3 \end{gathered}`

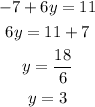
Thus, y=3

Answer: (7,3)