Question

Problem 1: Verify whether these two functions are inverses: f(x) = (x + 5)/(2x+1) and g(x) = (5-x)/(2x-1) What is g(f(x))? Where do i start? Do I need to find the inverses first?

Answer 1

f(x) and g(x) are inverse functions because:

f(g(x)) = x and g(f(x)) = x

Step-by-step explanation:

Two functions f(x) and g(x) are inverses if g(f(x)) = x and f(g(x)) = x.

So, f(x) and g(x) are equal to:

`\begin{gathered} f(x)=(x+5)/(2x+1) \\ g(x)=(5-x)/(2x-1) \end{gathered}`

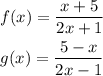
Then, to find g(f(x)), we need to replace x by f(x) on the equation of g(x), so we get:

`\begin{gathered} g(f(x))=(5-f(x))/(2f(x)-1) \\ g(f(x))=(5-(x+5)/(2x+1))/(2((x+5)/(2x+1))-1) \\ g(f(x))=((5(2x+1)-(x+5))/(2x+1))/((2(x+5)-1(2x+1))/(2x+1)) \\ g(f(x))=\frac{5(2x+1)-(x+5)}{2(x+5)-(2x+1)_{}} \\ g(f(x))=(10x+5-x-5)/(2x+10-2x-1) \\ g(f(x))=(9x)/(9)=x \end{gathered}`

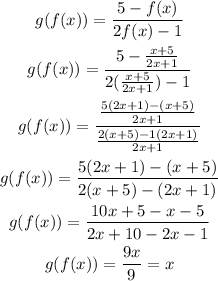
Now, we need to verify that f(g(x)) is also equal to x, so:

`\begin{gathered} f(g(x))=(g(x)+5)/(2g(x)+1) \\ f(g(x))=((5-x)/(2x-1)+5)/(2((5-x)/(2x+1))+1) \\ f(g(x))=((5-x+5(2x-1))/(2x-1))/((2(5-x)+1(2x-1))/(2x-1)) \\ f(g(x))=((5-x)+5(2x-1))/(2(5-x)+(2x-1)) \\ f(g(x))=(5-x+10x-5)/(10-2x+2x-1) \\ f(g(x))=(9x)/(9)=x \end{gathered}`

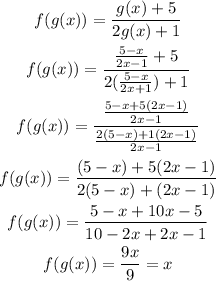
Since g(f(x)) and f(g(x)) are equal to x, we can say that f(x) ad g(x) are inverse functions.