Question

Find the external angle. (HINT: After you solve for x, plug it into the equation)

Answer 1

To find the external angle:-

At first we need to find the value of x.

We use the defnition, the angle of a straight line is 180 degree and since the equation of outer angle is (6x-7) the inner angle becomes 180 - (6x-7).

The diagram is,

So now we use the defnition the sum of three angles inside a triangle is 180 degree. so we get,

`\begin{gathered} 180-(6x-7)+103-x+2x=180 \\ 180-6x+7+103-x+2x=180 \\ 180-6x+110+x=180 \\ 290-5x=180 \\ -5x=180-290 \end{gathered}`

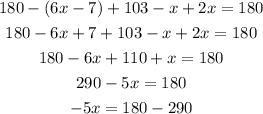
By furthur simplifying we get the value of x,

`\begin{gathered} -5x=180-290 \\ x=(-110)/(-5) \\ x=22 \end{gathered}`

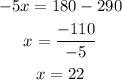
So the value of x is 22.

Subsituting the value of x in the equation ( 6x-7 ). we get the required angle value.

`\begin{gathered} 6x-7=6(22)-7 \\ \text{ =}132-7 \\ \text{ =125} \end{gathered}`

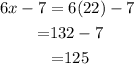
So the required angle value is 125 degree.