Question

What is the equation of the line graphed below?(2.1)O A. y = - 2xB. y = -2xC. y = 1/2D. y = 2x

Answer 1

The first step is to determine the slope of the line and that is calculated as follows;

`m=(y_2-y_1)/(x_2-x_1)`

Two points on the line have been identified as

`\begin{gathered} A=(0,0) \\ B=(2,1) \end{gathered}`

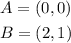
Note that the line passes through the origin which is (0, 0).

Therefore we now have;

`\begin{gathered} (x_1,y_1_{})=(0,0) \\ (x_2,y_2_{})=(2,1) \\ m=(1-0)/(2-0) \\ m=(1)/(2) \end{gathered}`

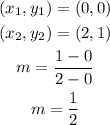
Now we have the slope determined as 1/2.

The y-intercept is derived as follows;

`\begin{gathered} \text{ Using the general equation of a straight line, which is;} \\ y=mx+b \\ b=y-\text{intercept} \\ We\text{ shall use point B=(2,1)} \\ 1=(1)/(2)(2)+b \\ 1=1+b \\ \text{Subtract 1 from both sides} \\ 0=b \end{gathered}`

We now have the values of m and b, the equation now becomes;

`\begin{gathered} y=mx+b \\ \text{Substitute for m=}(1)/(2),b=0 \\ y=(1)/(2)x+0 \\ y=(1)/(2)x \end{gathered}`

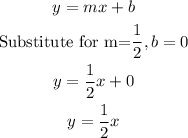
The correct answer therefore is option C