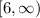Given the inequality:
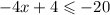
To solve the inequality for x, the first step is to subtract 4 from both sides of the inequality.
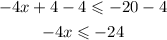
Next, we divide both sides of the inequality by -4.
Note: When you divide or multiply by a negative number in inequality, the inequality sign reverses.
Therefore, we have:
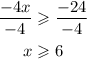
Next, we write our result in interval notation.
Since the value is greater than or equal to, we use the close bracket '['.
Therefore, the solution to the inequality in interval notation is: