Question

Utility Bills The monthly utility bills in a city are normally distributed and represented by the variable X, with a mean of $100 and a standard deviation of $12. Find the probability that a randomly selected utility bill is (a) less than $70, (b) between $90 and $120, (c) more than $140. Hint: Convert the normal distribution X to Standard normal using Z formula Z=(X-μ)/σ and then look the Z-values from the table and then find the probability.Can you help me step-by-step inserting the values to the formula it’s very confusing for me I don’t understand and I really need help I’m trying to study for my ged these are the exercises I was given to do

Answer 1

-Here is what we know:

The values of the monthly utility bills in a city are normally distributed

The mean is $100

The standard deviation is $12

Part a)

First, we must find the Z-score for x = $70:

`Z=(70-100)/(12)=-2.5`

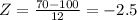
According to the Z-score table, the probability of finding x less than $70 such as z is less than -2.5 is P(Z < -2.5) = 1 - 0.9938 = 0.0062

Part b)

For x = $90, we repeat the same initial steps from part a:

`Z=(90-100)/(12)\approx-0.83`

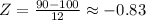
According to the Z-score table, we have P(Z <= -0.83) = 0.2033.

For x = $120, we also have:

`Z=(120-100)/(12)=1.67`

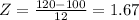
According to the Z-score table, we have P(Z < 1.67) = 0.9525

Therefore, the probability that we will fiind a bill valued between $90 and $120 is given by: P(Z < 1.67) - P(Z < -0.83) = 0.9525 - 0.2033 = 0.7492

Part c)

For X = $140, the z score is given by:

`Z=(140-100)/(12)\approx3.33`

According to the Z-score table, we have: P(Z > $140) = 1 - 0.9996 = 0.0004