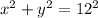SOLUTION
From the question, we are told that the circle pass through (12, 0) and centered at origin. So this means to find the radius, the diagram below would be helpful
From the diagram above, we have that
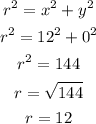
Equation of a circle is given as
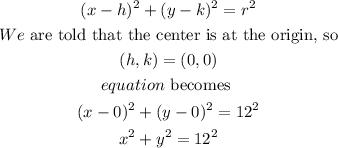
Hence the answer is