Question

An object moving with uniform acceleration has a velocity of 11.0 cm/s in the positive x-direction when its x-coordinate is 2.76 cm. If its x-coordinate 2.25 s later is −5.00 cm, what is its acceleration?

Answer 1

Given:

The initial velocity is

`v_i=\text{ 11 cm/s}`

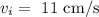
The initial position is x1 = 2.76 cm

The final position is x2 = - 5 cm

The time will be t = 2.25 s

To find the acceleration.

Step-by-step explanation:

The acceleration can be calculated by the formula

`\begin{gathered} \Delta x=v_it+(1)/(2)at^2 \\ (1)/(2)at^2=\Delta x-v_it \\ a=(2(\Delta x-v_it))/(t^2) \end{gathered}`

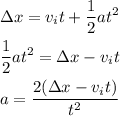
Here, the displacement is

`\begin{gathered} \Delta x=x2-x1 \\ =-5-2.76 \\ =-7.76\text{ cm} \end{gathered}`

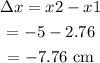
On substituting the values, the acceleration will be

`\begin{gathered} a=(2(-7.76-11*2.25))/((2.25)^2) \\ =\text{ -12.84 cm/s}^2 \end{gathered}`

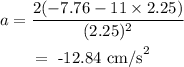
Final Answer: The acceleration is -12.84 cm/s^2