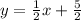SOLUTION
From the line
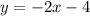
Comparing this to equation of a line in the form of
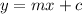
m= -2.
Let this be the first slope. Hence
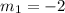
When two lines are perpendicular, their slope is related by the formula
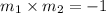
From here, we have that
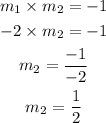
Equation of a line in lope-intercept form is give as
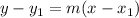
Using m2 to represent m in the equation we have
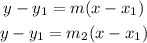
Where y1 = 4 and x1 = 3, our equation becomes
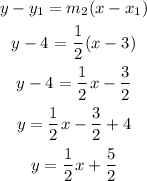
Hence the answer is