Answer:
(a)90
(b)(i) 10 (ii)6 (iii)5
Step-by-step explanation:
Part A
First, we find the lowest common multiple of 9,15, and 18.
To do this, express each number as a product of its prime factors.
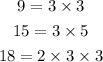
Next, multiply all prime factors the greatest number of times they occur in either number.

The LCM of 9, 15, and 18 is 90.
Part B
To answer this part, divide the LCM by the respective numbers:
(i)
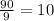
9 divides into LCM 10 times.
(ii)

15 divides into LCM 6 times.
(iii)
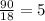
18 divides into LCM 5 times.