Question

May I please get help with this. I have tried multiple ways to get the answers but still could not get them right or correct

Answer 1

Step-by-step explanation

Step 1

as the lines that make the river are parallel the triangles are similar, so we can make a proportion

let

`\text{ratio = }\frac{\text{ opposite side}}{\text{adyancent side}}`

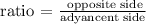
hence

`\begin{gathered} \text{ratio}_1=(16.2)/(33) \\ \end{gathered}`

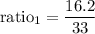
and let x represents the width of the river

`ratio_2=_{}(x)/(58)`

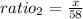
therefore, the proportion is

`\begin{gathered} \text{ ratio}_1=ratio_2 \\ (16.2)/(33)=(x)/(58) \\ \text{Multiply both sides by 58 to isolate x} \\ (16.2)/(33)\cdot58=(x)/(58)\cdot58 \\ 28.47=x \\ x=28.47 \\ \text{rounded to the nearest meter} \\ x=28\text{ meters} \end{gathered}`

so, the answer is

28 meters

I hope this helps you

,