Question

a garden table and a bench cost 573 combined. The garden table costs 77.00 less than the bench. what is the cost of the bench

Answer 1

Let 'x' represent the cost of the garden table.

Let 'y' represent the cost of the bench.

Therefore, from the first statemenet

`x+y=573\ldots\ldots.1`

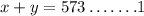
From the second statement,

`x=y-77\ldots\ldots2`

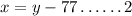
Substitute x = y - 77 into equation 1

`\begin{gathered} x+y=573 \\ y-77+y=573 \end{gathered}`

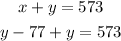
Collect like terms

`\begin{gathered} y+y=573+77 \\ 2y=650 \end{gathered}`

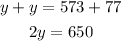
Divide both sides by 2

`\begin{gathered} (2y)/(2)=(650)/(2) \\ y=325 \end{gathered}`

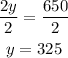
Therefore, the cost of the bench is 325.