Given: A circle with a diameter of 19 ft and a minor sector with a central angle of 123 degrees.
Required: To find out the area of a major sector.
Explanation: The area of the sector is given by the formula
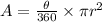
where,
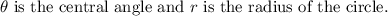
Now, the angle of the major sector (or the shaded region) can be found as follows,
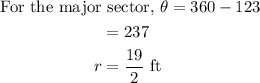
Now, the Area of the shaded region is
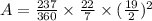
Which on simplification gives the result,
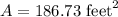
Final Answer: The area of the shaded region is 186.73 square feet.