Question

The first team of a GP is -20 and the 10th term is 10240. find S11 of this GP

Answer 1

Given that the first term of a GP is -20 and the 10th term is 10240.

We need to find S11 of this GP.

The first term is a = -20 and the tenth term is ar^9 = 10240. So,

`\begin{gathered} (ar^9)/(a)=(10240)/(-20) \\ r^9=-512 \\ r=(-512)^{(1)/(9)} \\ r=-2 \end{gathered}`

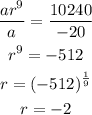
We know that the sum of n terms of gp is given by:

`S_n=(a(1-r^n))/((1-r))`

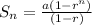
The sum of 11 terms of the gp is:

`\begin{gathered} S_(11)=\frac{-20(1-(-2)^(11)^{})}{1-(-2)} \\ =(-20(1-(-2048)))/(1+2) \\ =(-20(2049))/(3) \\ =-20(683) \\ =-13660 \end{gathered}`

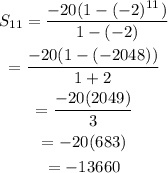
Thus, the value of S11 is -13660.