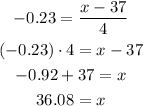Question

Suppose a set of data has a normal distribution withmean 37 and variance 16. What score has a percentile rankof 40.9%

Answer 1

A percentile rank of 40.9% corresponds to 0.409 in the above table which corresponds to a z-score of -0.23.

The z-score is computed as follows:

`z=(x-\mu)/(\sigma)`

where x is the observed value, μ is the mean and σ is the standard deviation.

In this case, the variance is 16, then the standard deviation is √16 = 4

Substituting into the z-score formula with z = -0.23, μ = 37, and σ = 4, we get:

`\begin{gathered} -0.23=(x-37)/(4) \\ (-0.23)\cdot4=x-37 \\ -0.92+37=x \\ 36.08=x \end{gathered}`