Question

3. [8 pts) Katie want to build a rectangular enclosure for your pet rabbit, Sniper, against the side of her house. She has bought 100 feet of fencing. What are the dimensions of the largest area that she can enclose?

Answer 1

Atrea of the rectangle = Length x Breadth

Perimeter = Length + the wall side + 2 x breadth

P = L + 0 + 2B (the wall side value is 0, because no fence is needed)

P = L + 2B

100 = L + 2B

L = 100 - 2B

`\begin{gathered} A\text{ = L x B} \\ \text{ = (100-2B) }* B\text{ } \\ \text{ = 100B - 2B}^2 \\ =-2B^2\text{ + 100B} \end{gathered}`

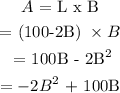
Since our equation for area in terms of widthis of the form ax^2 + bx + c (where C = 0), we have a parabola. Since the coefficient on the squared term is negative (a = -2), we know we have a parabola that opens downward. This means that we will have a maximum point at the vertex of the parabola, which is our maximum area.

We will say the vertex is at point (h, k), from the function y = (x - h)2 + k, in which k is our maximum area and h is our maximizing number: in this case, the value for width that gives us our maximum area.

We know h = -b / 2a.

`h\text{ =}(-100)/(2*-2)\text{ = }(-100)/(-4)=\text{ 20 ft}`

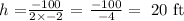
Therefore the B is 20 feet

`\begin{gathered} A=-2B^2\text{ + 100B} \\ \text{ = -2(20}^2)\text{ + 100 (20)} \\ =-800+2000=200ft^2 \end{gathered}`

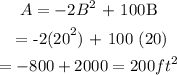
Since A = L X B

L = A/B =200/ 20 = 10 feet