Question

In 2010 online sales were $191 billion, and in 2014 they were $259 billion.a) Find a linear function S that models these data, where S is the sales in billions of dollars and x is the year. Write S(x) in slope-intercept form. b) Interpret the slope of the graph of S:A. Sales increased, on average, by $17 billion/yr.B. Sales increased by $17 billion in next 4 years.C. Sales decreased, on average, by $17 billion/yr.D. Sales decreased by $17 billion in next 4 years.c) Determine when online sales were $242 billion

Answer 1

According to the information given in the exercise:

- In 2010 online sales were ​$191 ​billion.

- In sales were $259 billion.

Let be "S" the sales in billions of dollars and "x" the year.

a) By definition, the Slope-Intercept Form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In order to find the slope, you need to apply the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where two points on the line are:

`\begin{gathered} (x_1,y_1) \\ (x_2,y_2) \end{gathered}`

In this case, you can identify these points on the line:

`\mleft(2010,191\mright);(2014,259)`

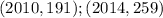
Then, you can find the slope as follows:

`m=(259-191)/(2014-2010)=(68)/(4)=17`

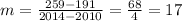
You can substitute the slope and the coordinates of one of the points on the line, into this equation:

`y=mx+b`

Then, you can solve for "b", in order to find the y-intercept:

`\begin{gathered} 191=(17)(2010)+b \\ \\ 191-34170=b \\ \\ b=-33979 \end{gathered}`

Knowing "m" and "b", you can write the following Linear Function in Slope-Intercept Form to model the given data:

`S(x)=17x-33979`

b) You know that the slope of the line of the function S is:

`m=17`

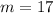
The slope of a line is defined as the change in "y" divided by the change in "x":

`m=(y_2-y_1)/(x_2-x_1)`

You know that, in this case, "S" (the sales in billions) is represented on the y-axis, and the variable "x" (the year) is represented on the x-axis.

Therefore, you can conclude that:

`m=(17)/(1)`

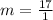
That indicates that the sales increased, on average, by $17 billion per year.

c) In order to determine when the online sales were ​$242 billion, you have to set up that:

`S(x)=242`

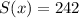
Hence, substituting this value into the function and solving for "x", you get:

`\begin{gathered} 242=17x-33979 \\ \\ 242+33979=17x \end{gathered}`
`\begin{gathered} 34221=17x \\ \\ (34221)/(17)=x \end{gathered}`
`x=2013`

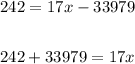
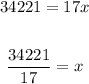
Therefore, the answers are:

a)

`S(x)=17x-33979`

b) Option A.

c) In 2013 the sales were $242 billion.