Given a matrix A of dimension (m × n), where m is the number of rows and n is the number of columns.
The transpose of matrix A is obtained by interchanging the rows and columns.
This implies that
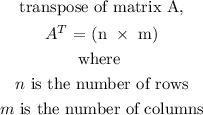
For two matrices to be conformable for multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix.
Thus, matrix A and its transpose are conformable since the number of columns in matrix A is equal to the number of rows in its transpose.

When the matrix A and its transpose are multiplied, we obtain a square and symmetric matrix.