Question

You are given that cos(A) = -15/17 with A in Quadrant III, and sin(B) = 4/5, with B in Quadrant II. Find sin(A - B). Give your answer as a fraction,.

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

Quadrant III:

cos (A) = -15 / 17

Step 02:

trig ratio:

cos θ = adjacent / hypotenuse

cos A = - 15 / 17

right triangle:

adjacent = 15

hypotenuse = 17

c² = a² + b²

17² = (15)² + (b)²

289 = 225 + b²

289 - 225 = b²

`\begin{gathered} \sqrt[]{64}\text{ = b} \\ 8\text{ = b} \end{gathered}`

opposite: 8

Quadrant III:

adjacent = -15

hypotenuse = 17

opposite = - 8

sin A = opposite / hypotenuse

sin A = - 8 / 17

sin (A - B):

`\sin \text{ (A -B)=}(-8)/(17)-(4)/(5)=(-40-68)/(85)=-(108)/(85)`

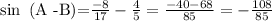
The answer is:

sin (A - B) = - 108 / 85