First, notice that since the point (a,1) belongs to the circumference x^2+y^2=5, then:
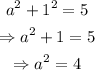
Since the point (a,1) is in the second quadrant, then:
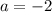
Remember that the coordinates of a point on a circle of radius r can be written in terms of the angle as:
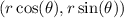
The radius of the circle in this case is the square root of 5. Then:
![(-2,1)=(\sqrt[]{5}\cos (\theta),\sqrt[]{5}\sin (\theta))](https://img.qammunity.org/2023/formulas/mathematics/college/pguef5cocggotlzhezoqq7wp8v4d55khhb.png)
Therefore:
![\begin{gathered} \sqrt[]{5}\cos (\theta)=-2 \\ \Rightarrow\cos (\theta)=-\frac{2}{\sqrt[]{5}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lxakvoo8io95r29djfw0dsyn6eoitcfnnh.png)
On the other hand, remember the following identity:
![\cos ((\theta)/(2))=\sqrt[]{(1+\cos (\theta))/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/nd0lhgosdc4bq6dj9czwa320885f9ue7g3.png)
Substitute the value for the cosine of θ:
![\begin{gathered} \cos ((\theta)/(2))=\sqrt[]{\frac{1-\frac{2}{\sqrt[]{5}}}{2}} \\ =\sqrt[]{\frac{\sqrt[]{5}-2}{2\sqrt[]{5}}} \\ =\sqrt[]{\frac{5-2\sqrt[]{5}}{10}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j8lfd5a9e0toilo9fk12v8jde9ktlg0cm9.png)
Therefore:
![g((\theta)/(2))=\sqrt[]{\frac{5-2\sqrt[]{5}}{10}}](https://img.qammunity.org/2023/formulas/mathematics/college/9atn4jkb0tifx2gbchgeos4puu73a6jj67.png)