Question

A lab cart with a mass of 560 grams has an initial speed of 1.83 meters per second. A constant force of 4.90 newtons is applied to the cart in the direction it's moving for 0.290 seconds. Friction gives the cart 0.308 newton·seconds of impulse in the opposite direction. What is the cart's final speed? Include units in your answer. Answer must be in 3 significant digits.

Answer 1

Given,

The mass of the cart, m=560 g=0.56 kg

The initial speed of the cart, u=1.83 m/s

The applied force, F=4.90 N

The time duration for which a constant force is applied, t=0.290 s

The impulse due to the friction, I=0.308 N

The impusle can be calculated as the product of the force and the period for which the force was applied.

Thus, the force acting on the cart due to friction is given by,

`f=(I)/(t)`

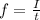
On substituting the known values,

`\begin{gathered} f=(0.308)/(0.209) \\ =1.47\text{ N} \end{gathered}`

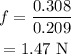
The net force acting on the cart is given by,

`F_n=ma=F-f`

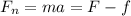
Where a is the acceleration of the cart due to these two forces.

On substituting the knwon values,

`\begin{gathered} 0.560* a=4.90-1.47 \\ \Rightarrow a=(3.43)/(0.560) \\ =6.13m/s^2 \end{gathered}`

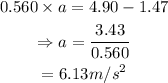
From the equation of the motion the final speed of the cart is,

`v=u+at`

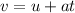
On substituting the known values,

`\begin{gathered} v=1.83+6.13*0.290 \\ =3.61\text{ m/s} \end{gathered}`

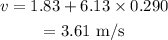
Thus the final speed of the cart is 3.61 m/s